Muitas vezes quando alguém está analisando dados distribuídos em subparcelas ou subamostras contíguas dentro de um bloco amostral ou transecção, um dos principais vieses a ser considerado é a pseudorepetição espacial. Neste caso, você precisa de um tipo de modelo chamado modelo misto que leva em consideração o viés de você possuir dados distribuídos em pseudoréplicas (ex: subparcelas). Muitos pesquisadores utilizam o GLMM (Generalized linear mixed models) na expectativa de conduzir uma análise estatística mais confiável. Como Dormann et al. (2007) mostram e argumentam, o GLMM pode ser uma forma de lidar com efeitos de autocorrelação espacial causados por pseudoreplicações, mas não necessariamente é a mais eficaz para corrigir esse efeito.
Um tipo de modelo de regressão mais eficiente que o GLMM neste aspecto é o LME (Linear mixed effects) do pacote “nlme”, o qual embasou primariamente o que veio a ser desenvolvido para o GLMM no pacote “lme4”. Não entraremos em detalhes específicos, mas há vários elementos que diferem o “nlme” e “lme4” e determinam as diferenças em eficiência entre LME e o GLMM. Mas, por exemplo, o “nlme” possui um aparato estatístico mais bem desenvolvido e robusto que permite ao LME corrigir efeitos de autocorrelações de forma geral devido a permitir especificar estruturas de correlação entre os resíduos, sendo a estrutura de correlação espacial exponencial (corExp) a mais usada. Apesar de seus modelos serem limitados a distribuição de erros gaussiana (normal), o pacote “nlme” permite modelar potencial heterocedasticidade e ajustar funções não-lineares. O pacote “lme4”, por outro lado é mais ágil computacionalmente, sendo mais amplo por permitir generalização para outras distribuições de erros (ex: poisson, binomial, negativo binomial) e recomendo principalmente para grandes banco de dados e quando vários efeitos aleatórios são considerados no modelo GLMM. No entanto, o “lme4” não permite especificar estruturas de correlação entre resíduos (a não ser pelos próprios efeitos aleatórios) ou lidar com heterocedasticidade como o “nlme” faz.
Nessa figura temos exemplo de um modelo LME sem a estrutura de correlação entre resíduos:
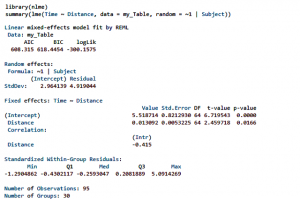
Já nessa figura abaixo temos exemplo de modelo nulo e “output” de um LME conduzido com uma estrutura de correlação espacial exponencial (CorExp) incluída:

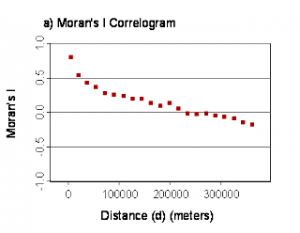
Uma forma de ainda aumentar a robustez estatística, utilizando o LME (selecionado como método base a “Maxmium Likelihood”) é fazendo um análise prévia do modelo desejado através de LM (Linear Models) para verificar se há significativa autocorrelação espacial. Esta verificação se faz inserindo esse LM no teste de Moran’s I usando o pacote “lctools”. Para isso, no seu arquivo de dados importado para o R, as subamostras (ex: subparcelas em estudos florestais) devem ter discriminadas duas colunas X e Y relativa às coordenadas UTM obtidas a partir das suas coordenadas geográficas originais. A partir dessas coordenadas UTM X e Y serão geradas coordenadas únicas para cada linha de dados e permitirá que o LM inserido no teste de Moran’s I aponte o nível (positiva ou negativa) e significância de autocorrelação espacial no seu modelo. O problema principal causado pela autocorrelação espacial nesse caso é agrupar resíduos no modelo, fazendo valores maiores se agruparem a maiores e menores a menores (autocorrelação positiva) ou aproximando valores maiores de valores menores e vice-versa (autocorrelação espacial negativa). A principal consequência desses efeitos de autocorrelação e aumento de erros estatísticos do tipo I, ou seja, rejeitar a hipótese nula quando ela é verdadeira, levando o executor da análise a considerar uma falsa relação significativa entre variável dependente e preditiva (s). Dessa forma, se após conduzir o teste I de Moran e o mesmo apontar significância (p<0.05) você deve inserir na sintaxe do seu LME a função “corExp”, por exemplo. Isto irá aumentar e inserir um fator de correção no LME, garantindo que você obtenha relações com p-valores confiáveis e robustos.
Esta publicação ajudou você a entender um pouco melhor sobre modelos mistos?
Você precisa de ajuda nessa escolha, criação, execução e interpretação d resultados nesse tipo de modelagem?
Deixe a Beta Analítica ajudá-lo (a) nessa tarefa =)
